SparkMLlib-Classification-and-Regression

本节涵盖分类和回归算法。它还包括讨论特定类别算法的部分，例如线性方法，树和集成方法。

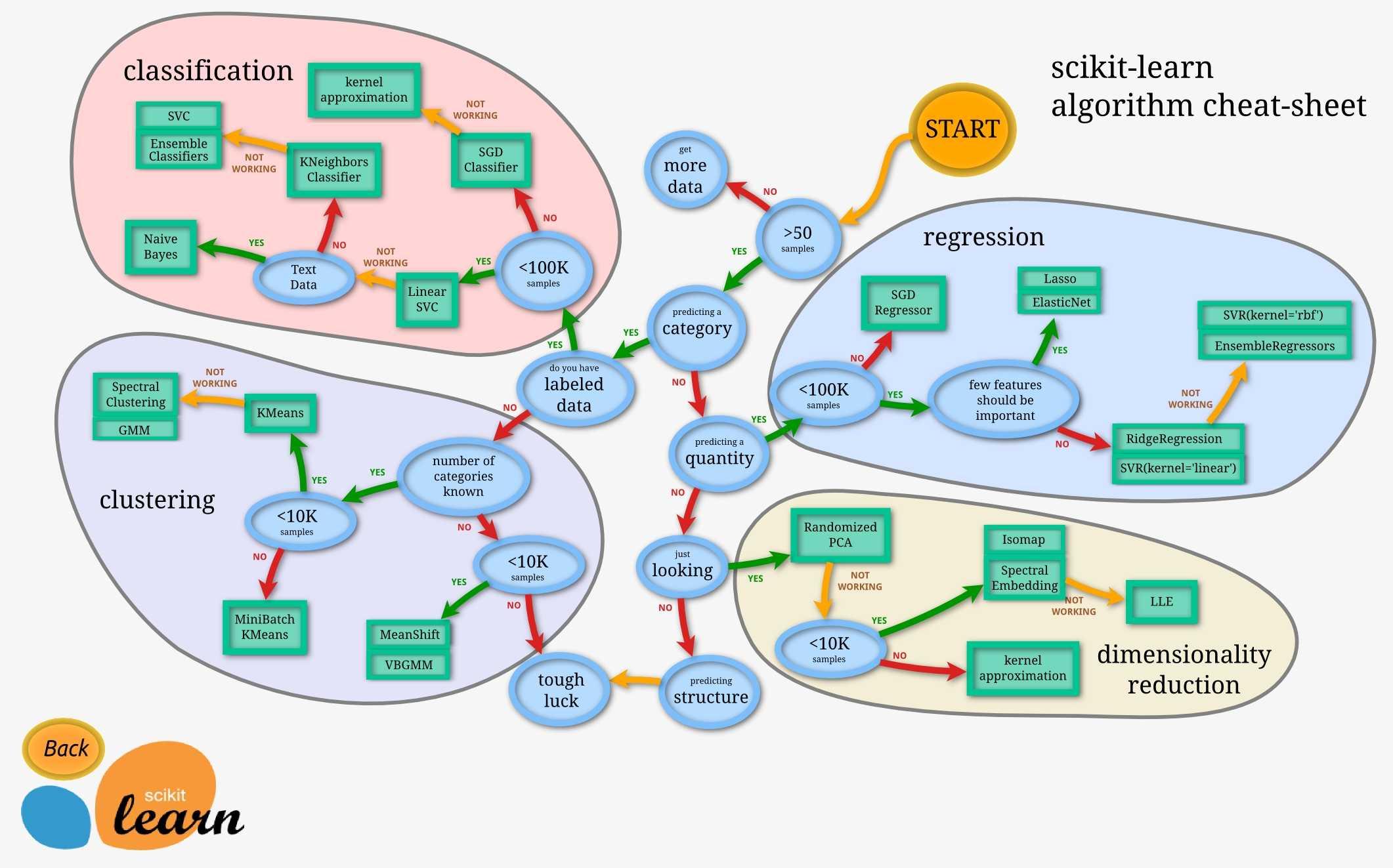
Classfication

Logistic Regression

Logistic Regression(逻辑回归)是一个流行的分类问题预测方法。它是Generalized Linear models(广义线性模型)的一个特殊应用以预测结果概率。在spark.ml逻辑回归中，可以使用二分类逻辑回归来预测二分类问题，或者可以使用多分类逻辑回归来预测多类别分类问题。使用family 参数来选择这两个算法，或者不设置，Spark会推断出正确的变量。

将family参数设置为“multinomial”时，多分类逻辑回归可以用于二分类问题。它会产生两套coeficients(w)和两个inercepts(b)。
当在具无拦截的连续非零列的数据集上训练LogisticRegressionModel时，Spark MLlib输出连续非零列零系数。这种行为与R glmnet相同，但与LIBSVM不同。

Binomial Logistic Regression

有关二项逻辑回归实现的更多背景和更多细节，请参阅中的logistic regression spark.mllib文档。

Examples

下面的例子显示了如何用弹性网络正则化的二元分类问题训练二项和多项逻辑回归模型。elasticNetParam参数对应于α(学习率)，regParam参数对应于λ(正则化参数)。有关参数的更多细节可以在Python API文档中找到。

from pyspark.ml.classification import LogisticRegression
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("LogisticRegressionWithElasticNetExample").getOrCreate()
# Load training data
training = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

lr = LogisticRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8)

# Fit the model
lrModel = lr.fit(training)

# Print the coefficients and intercept for logistic regression
print("Coefficients: " + str(lrModel.coefficients))
print("Intercept: " + str(lrModel.intercept))

# We can also use the multinomial family for binary classification
mlr = LogisticRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8, family="multinomial")

# Fit the model
mlrModel = mlr.fit(training)

# Print the coefficients and intercepts for logistic regression with multinomial family
print("Multinomial coefficients: " + str(mlrModel.coefficientMatrix))
print("Multinomial intercepts: " + str(mlrModel.interceptVector))
spark.stop()

output:

Coefficients: (692,[244,263,272,300,301,328,350,351,378,379,405,406,407,428,433,434,455,456,461,462,483,484,489,490,496,511,512,517,539,540,568],[-7.35398352419e-05,-9.10273850559e-05,-0.000194674305469,-0.000203006424735,-3.14761833149e-05,-6.84297760266e-05,1.58836268982e-05,1.40234970914e-05,0.00035432047525,0.000114432728982,0.000100167123837,0.00060141093038,0.000284024817912,-0.000115410847365,0.000385996886313,0.000635019557424,-0.000115064123846,-0.00015271865865,0.000280493380899,0.000607011747119,-0.000200845966325,-0.000142107557929,0.000273901034116,0.00027730456245,-9.83802702727e-05,-0.000380852244352,-0.000253151980086,0.000277477147708,-0.000244361976392,-0.00153947446876,-0.000230733284113])
Intercept: 0.22456315961250325
Multinomial coefficients: 2 X 692 CSRMatrix
(0,244) 0.0
(0,263) 0.0001
(0,272) 0.0001
(0,300) 0.0001
(0,350) -0.0
(0,351) -0.0
(0,378) -0.0
(0,379) -0.0
(0,405) -0.0
(0,406) -0.0006
(0,407) -0.0001
(0,428) 0.0001
(0,433) -0.0
(0,434) -0.0007
(0,455) 0.0001
(0,456) 0.0001
..
..
Multinomial intercepts: [-0.120658794459,0.120658794459]

Find full example code at “examples/src/main/python/ml/logistic_regression_with_elastic_net.py” in the Spark repo.

spark.ml逻辑回归工具还支持在训练集上提取模型的总结。请注意，在 BinaryLogisticRegressionSummary中存储为DataFrame的预测结果和指标被注释@transient(临时的)，因此仅适用于驱动程序。

LogisticRegressionTrainingSummary 为 LogisticRegressionModel提供了一个summary。目前只支持二分类问题。将来会增加对多分类问题模型summary的支持。

继续上面的例子

from pyspark.ml.classification import LogisticRegression
from pyspark.sql import SparkSession

spark = SparkSession \
    .builder \
    .appName("LogisticRegressionSummary") \
    .getOrCreate()

# Load training data
training = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

lr = LogisticRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8)

# Fit the model
lrModel = lr.fit(training)

# $example on$
# Extract the summary from the returned LogisticRegressionModel instance trained
# in the earlier example
trainingSummary = lrModel.summary

# Obtain the objective per iteration
objectiveHistory = trainingSummary.objectiveHistory
print("objectiveHistory:")
for objective in objectiveHistory:
    print(objective)

# Obtain the receiver-operating characteristic as a dataframe and areaUnderROC.
trainingSummary.roc.show()
print("areaUnderROC: " + str(trainingSummary.areaUnderROC))

# Set the model threshold to maximize F-Measure
fMeasure = trainingSummary.fMeasureByThreshold
maxFMeasure = fMeasure.groupBy().max('F-Measure').select('max(F-Measure)').head()
bestThreshold = fMeasure.where(fMeasure['F-Measure'] == maxFMeasure['max(F-Measure)']) \
    .select('threshold').head()['threshold']
lr.setThreshold(bestThreshold)
# $example off$

spark.stop()

output:

objectiveHistory:
0.6833149135741672
0.6662875751473734
0.6217068546034618
0.6127265245887887
0.6060347986802873
0.6031750687571562
0.5969621534836274
0.5940743031983118
0.5906089243339022
0.5894724576491042
0.5882187775729587
+---+--------------------+
|FPR|                 TPR|
+---+--------------------+
|0.0|                 0.0|
|0.0|0.017543859649122806|
|0.0| 0.03508771929824561|
|0.0| 0.05263157894736842|
|0.0| 0.07017543859649122|
|0.0| 0.08771929824561403|
|0.0| 0.10526315789473684|
|0.0| 0.12280701754385964|
|0.0| 0.14035087719298245|
|0.0| 0.15789473684210525|
|0.0| 0.17543859649122806|
|0.0| 0.19298245614035087|
|0.0| 0.21052631578947367|
|0.0| 0.22807017543859648|
|0.0| 0.24561403508771928|
|0.0|  0.2631578947368421|
|0.0|  0.2807017543859649|
|0.0|  0.2982456140350877|
|0.0|  0.3157894736842105|
|0.0|  0.3333333333333333|
+---+--------------------+
only showing top 20 rows

areaUnderROC: 1.0

Find full example code at “examples/src/main/python/ml/logistic_regression_summary_example.py” in the Spark repo.

Multinomial Logistic Regression

多分类通过多项逻辑（softmax）回归来支持。在多项逻辑回归中，算法产生K sets的系数集合(类似机器学习中的W)或维度K × J的矩阵其中K是结果分类数量和J是特征的数量。如果算法拟合时使用了偏置(类似机器学习中的b)，则偏置b也是一个K长度的向量。

多项逻辑回归的系数(coefficients)：coefficientMatrix，偏置(intercepts):interceptVector。
coefficients和intercept在用多项逻辑回归训练模型中不适用。请使用coefficientMatrix，interceptVector

结果的条件概率使用的是softmax function建模，我们使用多分类响应模型将加权负对数似然最小化，并使用elastic-net penalty来控制过拟合。

Multinomial Logistic Regression
关于推导的细节请查阅这里.

下面的例子展示了如何训练具有弹性网络正则化的多类逻辑回归模型。

from pyspark.ml.classification import LogisticRegression
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("MultinomialLogisticRegression").getOrCreate()
# Load training data
training = spark \
    .read \
    .format("libsvm") \
    .load("data/mllib/sample_multiclass_classification_data.txt")

lr = LogisticRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8)

# Fit the model
lrModel = lr.fit(training)

# Print the coefficients and intercept for multinomial logistic regression
print("Coefficients: \n" + str(lrModel.coefficientMatrix))
print("Intercept: " + str(lrModel.interceptVector))
spark.stop()

output:

Coefficients: 
3 X 4 CSRMatrix
(0,3) 0.3176
(1,2) -0.7804
(1,3) -0.377
Intercept: [0.0516523165983,-0.123912249909,0.0722599333102]

Find full example code at “examples/src/main/python/ml/multiclass_logistic_regression_with_elastic_net.py” in the Spark repo.

Decision Tree Classifier

决策树是一种流行的分类和回归方法。关于spark.ml实现的更多信息可以在决策树部分进一步找到。

Examples

以下示例以LibSVM格式加载数据集，将其分解为训练集和测试集，在训练数据集上训练，然后在保留的测试集上进行评估。我们使用两个特征变换器来准备数据; 这些帮助建立对标签和分类特征的索引，添加元数据到决策树算法可以识别的DataFrame上。

from pyspark.ml import Pipeline
from pyspark.ml.classification import DecisionTreeClassifier
from pyspark.ml.feature import StringIndexer, VectorIndexer
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("DecisionTreeExample").getOrCreate()
# Load the data stored in LIBSVM format as a DataFrame.
data = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

# Index labels, adding metadata to the label column.
# Fit on whole dataset to include all labels in index.
labelIndexer = StringIndexer(inputCol="label", outputCol="indexedLabel").fit(data)
# Automatically identify categorical features, and index them.
# We specify maxCategories so features with > 4 distinct values are treated as continuous.
featureIndexer =\
    VectorIndexer(inputCol="features", outputCol="indexedFeatures", maxCategories=4).fit(data)

# Split the data into training and test sets (30% held out for testing)
(trainingData, testData) = data.randomSplit([0.7, 0.3])

# Train a DecisionTree model.
dt = DecisionTreeClassifier(labelCol="indexedLabel", featuresCol="indexedFeatures")

# Chain indexers and tree in a Pipeline
pipeline = Pipeline(stages=[labelIndexer, featureIndexer, dt])

# Train model.  This also runs the indexers.
model = pipeline.fit(trainingData)

# Make predictions.
predictions = model.transform(testData)

# Select example rows to display.
predictions.select("prediction", "indexedLabel", "features").show(5)

# Select (prediction, true label) and compute test error
evaluator = MulticlassClassificationEvaluator(
    labelCol="indexedLabel", predictionCol="prediction", metricName="accuracy")
accuracy = evaluator.evaluate(predictions)
print("Test Error = %g " % (1.0 - accuracy))

treeModel = model.stages[2]
# summary only
print(treeModel)
spark.stop()

output:

+----------+------------+--------------------+
|prediction|indexedLabel|            features|
+----------+------------+--------------------+
|       1.0|         1.0|(692,[95,96,97,12...|
|       1.0|         1.0|(692,[100,101,102...|
|       1.0|         1.0|(692,[122,123,124...|
|       1.0|         1.0|(692,[125,126,127...|
|       1.0|         1.0|(692,[126,127,128...|
+----------+------------+--------------------+
only showing top 5 rows

Test Error = 0.0454545 
DecisionTreeClassificationModel (uid=DecisionTreeClassifier_4b29a1e1d3b0e6e09baf) of depth 1 with 3 nodes

Find full example code at “examples/src/main/python/ml/decision_tree_classification_example.py” in the Spark repo.

Random Forest Classifier

随机森林是一种流行的分类和回归方法。关于spark.ml实现的更多信息可以在关于随机森林的章节中进一步找到。

Examples

以下示例以LibSVM格式加载数据集，将其分解为训练集和测试集，在训练数据集上训练，然后在测试集上进行评估。我们使用两个特征变换器来准备数据,这有助于帮助索引标签和分类特征的类别，添加元数据到DtaFrame(基于树的算法可以识别的)。

from pyspark.ml import Pipeline
from pyspark.ml.classification import RandomForestClassifier
from pyspark.ml.feature import IndexToString, StringIndexer, VectorIndexer
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName('RandomForestExample').getOrCreate()
# Load and parse the data file, converting it to a DataFrame.
data = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

# Index labels, adding metadata to the label column.
# Fit on whole dataset to include all labels in index.
labelIndexer = StringIndexer(inputCol="label", outputCol="indexedLabel").fit(data)

# Automatically identify categorical features, and index them.
# Set maxCategories so features with > 4 distinct values are treated as continuous.
featureIndexer =\
    VectorIndexer(inputCol="features", outputCol="indexedFeatures", maxCategories=4).fit(data)

# Split the data into training and test sets (30% held out for testing)
(trainingData, testData) = data.randomSplit([0.7, 0.3])

# Train a RandomForest model.
rf = RandomForestClassifier(labelCol="indexedLabel", featuresCol="indexedFeatures", numTrees=10)

# Convert indexed labels back to original labels.
labelConverter = IndexToString(inputCol="prediction", outputCol="predictedLabel",
                               labels=labelIndexer.labels)

# Chain indexers and forest in a Pipeline
pipeline = Pipeline(stages=[labelIndexer, featureIndexer, rf, labelConverter])

# Train model.  This also runs the indexers.
model = pipeline.fit(trainingData)

# Make predictions.
predictions = model.transform(testData)

# Select example rows to display.
predictions.select("predictedLabel", "label", "features").show(5)

# Select (prediction, true label) and compute test error
evaluator = MulticlassClassificationEvaluator(
    labelCol="indexedLabel", predictionCol="prediction", metricName="accuracy")
accuracy = evaluator.evaluate(predictions)
print("Test Error = %g" % (1.0 - accuracy))

rfModel = model.stages[2]
print(rfModel)  # summary only
spark.stop()

output:

+--------------+-----+--------------------+
|predictedLabel|label|            features|
+--------------+-----+--------------------+
|           0.0|  0.0|(692,[98,99,100,1...|
|           1.0|  0.0|(692,[100,101,102...|
|           0.0|  0.0|(692,[124,125,126...|
|           0.0|  0.0|(692,[124,125,126...|
|           0.0|  0.0|(692,[124,125,126...|
+--------------+-----+--------------------+
only showing top 5 rows

Test Error = 0.0416667
RandomForestClassificationModel (uid=RandomForestClassifier_4e8ca5bee5432b4471d3) with 10 trees

Find full example code at “examples/src/main/python/ml/random_forest_classifier_example.py” in the Spark repo.

Gradient-Boosted Tree Classifier

Gradient-boosted trees (GBTs) 是一种流行的分类和回归方法，是一种决策树的集成算法。关于spark.ml实现的更多信息可以在GBT的一节中找到。

Examples

from pyspark.ml import Pipeline
from pyspark.ml.classification import GBTClassifier
from pyspark.ml.feature import StringIndexer, VectorIndexer
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName('GBTExample').getOrCreate()
# Load and parse the data file, converting it to a DataFrame.
data = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

# Index labels, adding metadata to the label column.
# Fit on whole dataset to include all labels in index.
labelIndexer = StringIndexer(inputCol="label", outputCol="indexedLabel").fit(data)
# Automatically identify categorical features, and index them.
# Set maxCategories so features with > 4 distinct values are treated as continuous.
featureIndexer =\
    VectorIndexer(inputCol="features", outputCol="indexedFeatures", maxCategories=4).fit(data)

# Split the data into training and test sets (30% held out for testing)
(trainingData, testData) = data.randomSplit([0.7, 0.3])

# Train a GBT model.
gbt = GBTClassifier(labelCol="indexedLabel", featuresCol="indexedFeatures", maxIter=10)

# Chain indexers and GBT in a Pipeline
pipeline = Pipeline(stages=[labelIndexer, featureIndexer, gbt])

# Train model.  This also runs the indexers.
model = pipeline.fit(trainingData)

# Make predictions.
predictions = model.transform(testData)

# Select example rows to display.
predictions.select("prediction", "indexedLabel", "features").show(5)

# Select (prediction, true label) and compute test error
evaluator = MulticlassClassificationEvaluator(
    labelCol="indexedLabel", predictionCol="prediction", metricName="accuracy")
accuracy = evaluator.evaluate(predictions)
print("Test Error = %g" % (1.0 - accuracy))

gbtModel = model.stages[2]
print(gbtModel)  # summary only
spark.stop()

output:

+----------+------------+--------------------+
|prediction|indexedLabel|            features|
+----------+------------+--------------------+
|       1.0|         1.0|(692,[98,99,100,1...|
|       1.0|         1.0|(692,[100,101,102...|
|       1.0|         1.0|(692,[124,125,126...|
|       1.0|         1.0|(692,[124,125,126...|
|       1.0|         1.0|(692,[124,125,126...|
+----------+------------+--------------------+
only showing top 5 rows

Test Error = 0.030303
GBTClassificationModel (uid=GBTClassifier_439db0c5094b1786e321) with 10 trees

Find full example code at “examples/src/main/python/ml/gradient_boosted_tree_classifier_example.py” in the Spark repo

Multilayer Perception Classifier

多层感知器分类器（MLPC）是基于前馈人工神经网络的分类器。MLPC由多层节点组成。每层完全连接到网络中的下一层。输入层中的节点表示输入数据。所有其他节点通过输入与节点权重w 和偏差b的线性组合并应用激活函数将输入映射到输出。K + 1层的MPLC可写成如下的矩阵形式：
MLPC

中间层节点使用sigmoid（logistic）函数：f(zi) = 1/(1 + e^-zi)\
输出层中的节点使用softmax函数：f(zi) = e^zi/(∑e^zi) \
输出层中N代表类别数目\
多层感知机通过方向向传播来学习模型，我们使用逻辑损失函数优化,L-BFGS作为优化程序.

from pyspark.ml.classification import MultilayerPerceptronClassifier
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName('MLPCExample').getOrCreate()
# Load training dat
data = spark.read.format("libsvm")\
    .load("data/mllib/sample_multiclass_classification_data.txt")

# Split the data into train and test
splits = data.randomSplit([0.6, 0.4], 1234)
train = splits[0]
test = splits[1]

# specify layers for the neural network:
# input layer of size 4 (features), two intermediate of size 5 and 4
# and output of size 3 (classes)
layers = [4, 5, 4, 3]

# create the trainer and set its parameters
trainer = MultilayerPerceptronClassifier(maxIter=100, layers=layers, blockSize=128, seed=1234)

# train the model
model = trainer.fit(train)

# compute accuracy on the test set
result = model.transform(test)
predictionAndLabels = result.select("prediction", "label")
evaluator = MulticlassClassificationEvaluator(metricName="accuracy")
print("Test set accuracy = " + str(evaluator.evaluate(predictionAndLabels)))
spark.stop()

output:

1	Test set accuracy = 0.8627450980392157

Find full example code at “examples/src/main/python/ml/multilayer_perceptron_classification.py” in the Spark repo.

Linear Support Vector Machine

一个支持向量机在高或无限维空间构建一个或一簇超平面，该空间可用于分类，回归或其他任务。直觉上，通过寻找距离任何类别的最近的训练数据点（所谓的functional margin）最大距离的超平面来实现良好的分离，因为一般而言，margin越大，分类器的泛化误差越低。Spark ML中的LinearSVC支持线性SVM的二元分类。在内部，它使用OWLQN优化器来优化hinge loss。


from pyspark.ml.classification import LinearSVC
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("linearSVCExample").getOrCreate()
# Load training data
training = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

lsvc = LinearSVC(maxIter=10, regParam=0.1)

# Fit the model
lsvcModel = lsvc.fit(training)

# Print the coefficients and intercept for linearsSVC
print("Coefficients: " + str(lsvcModel.coefficients))
print("Intercept: " + str(lsvcModel.intercept))
spark.stop()

output:


Coefficients:
[0.0,0.0,......,-5.83656045253e-05,-0.000123781942165,-0.000117507049533,-6.19711523061e-05,-5.04200964581e-05,-0.000140552602236,-0.000141033094247,-0.000192723082389,-0.000480248996468]
Intercept: 0.012911305214513969

Find full example code at “examples/src/main/python/ml/linearsvc.py” in the Spark repo.

One-vs-Rest Classifier(又叫 One-vs-All)

OneVsRest是一个将一个给定的二分类算法有效地扩展到多分类问题应用中的算法，也叫做“One-vs-All”算法。

OneVsRest是一个被实现为Estimator。它采用一个基础的Classifier然后对于k个类别分别创建二分类问题。类别i的二分类分类器用来预测类别为i还是不为i，即将i类和其他类别区分开来。最后，通过依次对k个二分类分类器进行评估，取置信最高的分类器的标签作为i类别的标签。

Examples

下面的示例演示了如何加载Iris数据集，将其解析为DataFrame并使用其执行多类别分类OneVsRest。计算测试误差以测量算法精度。


from pyspark.ml.classification import LogisticRegression, OneVsRest
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("oneVsRestExample").getOrCreate()
# load data file.
inputData = spark.read.format("libsvm") \
    .load("data/mllib/sample_multiclass_classification_data.txt")

# generate the train/test split.
(train, test) = inputData.randomSplit([0.8, 0.2])

# instantiate the base classifier.
lr = LogisticRegression(maxIter=10, tol=1E-6, fitIntercept=True)

# instantiate the One Vs Rest Classifier.
ovr = OneVsRest(classifier=lr)

# train the multiclass model.
ovrModel = ovr.fit(train)

# score the model on test data.
predictions = ovrModel.transform(test)

# obtain evaluator.
evaluator = MulticlassClassificationEvaluator(metricName="accuracy")

# compute the classification error on test data.
accuracy = evaluator.evaluate(predictions)
print("Test Error = %g" % (1.0 - accuracy))
spark.stop()

output:

1 2	Test Error = 0.0625

Find full example code at “examples/src/main/python/ml/one_vs_rest_example.py” in the Spark repo.

Naive Bayes

朴素贝叶斯分类器是一个简单的基于贝叶斯定理与特征条件独立假设的概率分类器。spark.ml目前的实现支持多项式朴素贝叶斯和伯努利朴素贝叶斯。更多的信息可以在MLlib的Naive Bayes一节中找到。


from pyspark.ml.classification import NaiveBayes
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("NaiveBayesExample").getOrCreate()
# Load training data
data = spark.read.format("libsvm") \
    .load("data/mllib/sample_libsvm_data.txt")

# Split the data into train and test
splits = data.randomSplit([0.6, 0.4], 1234)
train = splits[0]
test = splits[1]

# create the trainer and set its parameters
nb = NaiveBayes(smoothing=1.0, modelType="multinomial")

# train the model
model = nb.fit(train)

# select example rows to display.
predictions = model.transform(test)
predictions.show()

# compute accuracy on the test set
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction",
                                              metricName="accuracy")
accuracy = evaluator.evaluate(predictions)
print("Test set accuracy = " + str(accuracy))
spark.stop()

output:


+-----+--------------------+--------------------+-----------+----------+
|label|            features|       rawPrediction|probability|prediction|
+-----+--------------------+--------------------+-----------+----------+
|  0.0|(692,[95,96,97,12...|[-174115.98587057...|  [1.0,0.0]|       0.0|
|  0.0|(692,[98,99,100,1...|[-178402.52307196...|  [1.0,0.0]|       0.0|
|  0.0|(692,[100,101,102...|[-100905.88974016...|  [1.0,0.0]|       0.0|
|  0.0|(692,[123,124,125...|[-244784.29791241...|  [1.0,0.0]|       0.0|
|  0.0|(692,[123,124,125...|[-196900.88506109...|  [1.0,0.0]|       0.0|
|  0.0|(692,[124,125,126...|[-238164.45338794...|  [1.0,0.0]|       0.0|
|  0.0|(692,[124,125,126...|[-184206.87833381...|  [1.0,0.0]|       0.0|
|  0.0|(692,[127,128,129...|[-214174.52863813...|  [1.0,0.0]|       0.0|
|  0.0|(692,[127,128,129...|[-182844.62193963...|  [1.0,0.0]|       0.0|
|  0.0|(692,[128,129,130...|[-246557.10990301...|  [1.0,0.0]|       0.0|
|  0.0|(692,[152,153,154...|[-208282.08496711...|  [1.0,0.0]|       0.0|
|  0.0|(692,[152,153,154...|[-243457.69885665...|  [1.0,0.0]|       0.0|
|  0.0|(692,[153,154,155...|[-260933.50931276...|  [1.0,0.0]|       0.0|
|  0.0|(692,[154,155,156...|[-220274.72552901...|  [1.0,0.0]|       0.0|
|  0.0|(692,[181,182,183...|[-154830.07125175...|  [1.0,0.0]|       0.0|
|  1.0|(692,[99,100,101,...|[-145978.24563975...|  [0.0,1.0]|       1.0|
|  1.0|(692,[100,101,102...|[-147916.32657832...|  [0.0,1.0]|       1.0|
|  1.0|(692,[123,124,125...|[-139663.27471685...|  [0.0,1.0]|       1.0|
|  1.0|(692,[124,125,126...|[-129013.44238751...|  [0.0,1.0]|       1.0|
|  1.0|(692,[125,126,127...|[-81829.799906049...|  [0.0,1.0]|       1.0|
+-----+--------------------+--------------------+-----------+----------+
only showing top 20 rows

Test set accuracy = 1.0

Find full example code at “examples/src/main/python/ml/naive_bayes_example.py” in the Spark repo.

Regression

Linear regression

用于处理线性回归模型和模型摘要的界面与逻辑回归情况类似。

When fitting LinearRegressionModel without intercept on dataset with constant nonzero column by “l-bfgs” solver, Spark MLlib outputs zero coefficients for constant nonzero columns. This behavior is the same as R glmnet but different from LIBSVM.
Examples

下面的例子演示了训练弹性网络正则化线性回归模型和提取模型总结统计。


from pyspark.ml.regression import LinearRegression
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("LinearRegressionExample").getOrCreate()
# Load training data
training = spark.read.format("libsvm")\
    .load("data/mllib/sample_linear_regression_data.txt")

lr = LinearRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8)

# Fit the model
lrModel = lr.fit(training)

# Print the coefficients and intercept for linear regression
print("Coefficients: %s" % str(lrModel.coefficients))
print("Intercept: %s" % str(lrModel.intercept))

# Summarize the model over the training set and print out some metrics
trainingSummary = lrModel.summary
print("numIterations: %d" % trainingSummary.totalIterations)
print("objectiveHistory: %s" % str(trainingSummary.objectiveHistory))
trainingSummary.residuals.show()
print("RMSE: %f" % trainingSummary.rootMeanSquaredError)
print("r2: %f" % trainingSummary.r2)
spark.stop()

output:


Coefficients: [0.0,0.322925166774,-0.343854803456,1.91560170235,0.0528805868039,0.76596272046,0.0,-0.151053926692,-0.215879303609,0.220253691888]
Intercept: 0.1598936844239736
numIterations: 7
objectiveHistory: [0.49999999999999994, 0.4967620357443381, 0.4936361664340463, 0.4936351537897608, 0.4936351214177871, 0.49363512062528014, 0.4936351206216114]
+--------------------+
|           residuals|
+--------------------+
|  -9.889232683103197|
|  0.5533794340053554|
|  -5.204019455758823|
| -20.566686715507508|
|    -9.4497405180564|
|  -6.909112502719486|
|  -10.00431602969873|
|   2.062397807050484|
|  3.1117508432954772|
| -15.893608229419382|
|  -5.036284254673026|
|   6.483215876994333|
|  12.429497299109002|
|  -20.32003219007654|
| -2.0049838218725005|
| -17.867901734183793|
|   7.646455887420495|
| -2.2653482182417406|
|-0.10308920436195645|
|  -1.380034070385301|
+--------------------+
only showing top 20 rows

RMSE: 10.189077
r2: 0.022861

Find full example code at “examples/src/main/python/ml/linear_regression_with_elastic_net.py” in the Spark repo.

Generalized linear regression

与线性回归假设输出服从高斯分布不同，广义线性模型（GLMs）指定线性模型的因变量服从指数分布。
Spark的GeneralizedLinearRegression接口允许指定GLMs包括线性回归、泊松回归、逻辑回归等来处理多种预测问题。目前spark.ml仅支持指数型分布家族中的一部分类型，如下：

Family	Response Type	Supported Links
Gaussian(高斯)	Continuous(连续)	Identity*, Log, Inverse
Binomial(二项)	Binary(二进制)	Logit*, Probit, CLogLog
Poisson(泊松)	Count(计数)	Log*, Identity, Sqrt
Gamma(伽马)	Continuous(连续)	Inverse*, Idenity, Log
Tweedie	Zero-inflated continuous(零膨胀连续)	Power link function

注意：目前Spark在 GeneralizedLinearRegression仅支持最多4096个特征，如果特征超过4096个将会引发异常。对于线性回归和逻辑回归，如果模型特征数量会不断增长，则可通过 LinearRegression 和LogisticRegression来训练。

GLMs要求的指数型分布可以为正则或者自然形式。自然指数型分布为如下形式：
广义线性模型

Spark的GeneralizedLinearRegression接口提供汇总统计来诊断GLM模型的拟合程度，包括残差、p值、残差、Akaike信息准则及其它。

Examples

以下示例演示使用高斯响应和标识链接函数训练GLM并提取模型摘要统计信息。


from pyspark.ml.regression import GeneralizedLinearRegression
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("GeneralizedLinearRegression").getOrCreate()
# Load training data
dataset = spark.read.format("libsvm")\
    .load("data/mllib/sample_linear_regression_data.txt")

glr = GeneralizedLinearRegression(family="gaussian", link="identity", maxIter=10, regParam=0.3)

# Fit the model
model = glr.fit(dataset)

# Print the coefficients and intercept for generalized linear regression model
print("Coefficients: " + str(model.coefficients))
print("Intercept: " + str(model.intercept))

# Summarize the model over the training set and print out some metrics
summary = model.summary
print("Coefficient Standard Errors: " + str(summary.coefficientStandardErrors))
print("T Values: " + str(summary.tValues))
print("P Values: " + str(summary.pValues))
print("Dispersion: " + str(summary.dispersion))
print("Null Deviance: " + str(summary.nullDeviance))
print("Residual Degree Of Freedom Null: " + str(summary.residualDegreeOfFreedomNull))
print("Deviance: " + str(summary.deviance))
print("Residual Degree Of Freedom: " + str(summary.residualDegreeOfFreedom))
print("AIC: " + str(summary.aic))
print("Deviance Residuals: ")
summary.residuals().show()
spark.stop()

output:


Coefficients: [0.0105418280813,0.800325310056,-0.784516554142,2.36798871714,0.501000208986,1.12223511598,-0.292682439862,-0.498371743232,-0.603579718068,0.672555006719]
Intercept: 0.14592176145232041
Coefficient Standard Errors: [0.7950428434287478, 0.8049713176546897, 0.7975916824772489, 0.8312649247659919, 0.7945436200517938, 0.8118992572197593, 0.7919506385542777, 0.7973378214726764, 0.8300714999626418, 0.7771333489686802, 0.463930109648428]
T Values: [0.013259446542269243, 0.9942283563442594, -0.9836067393599172, 2.848657084633759, 0.6305509179635714, 1.382234441029355, -0.3695715687490668, -0.6250446546128238, -0.7271418403049983, 0.8654306337661122, 0.31453393176593286]
P Values: [0.989426199114056, 0.32060241580811044, 0.3257943227369877, 0.004575078538306521, 0.5286281628105467, 0.16752945248679119, 0.7118614002322872, 0.5322327097421431, 0.467486325282384, 0.3872259825794293, 0.753249430501097]
Dispersion: 105.60988356821714
Null Deviance: 53229.3654338832
Residual Degree Of Freedom Null: 500
Deviance: 51748.8429484264
Residual Degree Of Freedom: 490
AIC: 3769.1895871765314
Deviance Residuals: 
+-------------------+
|  devianceResiduals|
+-------------------+
|-10.974359174246889|
| 0.8872320138420559|
| -4.596541837478908|
|-20.411667435019638|
|-10.270419345342642|
|-6.0156058956799905|
|-10.663939415849267|
| 2.1153960525024713|
| 3.9807132379137675|
|-17.225218272069533|
| -4.611647633532147|
| 6.4176669407698546|
| 11.407137945300537|
| -20.70176540467664|
| -2.683748540510967|
|-16.755494794232536|
|  8.154668342638725|
|-1.4355057987358848|
|-0.6435058688185704|
|  -1.13802589316832|
+-------------------+
only showing top 20 rows

Find full example code at “examples/src/main/python/ml/generalized_linear_regression_example.py” in the Spark repo.

Decision tree regression

决策树以及其集成算法是机器学习分类和回归问题中非常流行的算法。因其易解释性、可处理类别特征、易扩展到多分类问题、不需特征缩放等性质被广泛使用。树集成算法如随机森林以及boosting算法几乎是解决分类和回归问题中表现最优的算法。

决策树是一个贪心算法递归地将特征空间划分为两个部分，在同一个叶子节点的数据最后会拥有同样的标签。每次划分通过贪心的以获得最大信息增益为目的，从可选择的分裂方式中选择最佳的分裂节点。节点不纯度有节点所含类别的同质性来衡量。工具提供为分类提供两种不纯度衡量（基尼不纯度和熵），为回归提供一种不纯度衡量（方差）。

spark.ml支持二分类、多分类以及回归的决策树算法，适用于连续特征以及类别特征。另外，对于分类问题，工具可以返回属于每种类别的概率（类别条件概率），对于回归问题工具可以返回预测在偏置样本上的方差。

Examples

以下示例以LibSVM格式加载数据集，将其分为训练集和测试集，在训练集训练，然后在测试集上进行评估。我们使用特征转换器为分类特征建立索引，并将元数据添加到DataFrame供决策树算法使用。


from pyspark.ml import Pipeline
from pyspark.ml.regression import DecisionTreeRegressor
from pyspark.ml.feature import VectorIndexer
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("DecisionTreeRegressionExample").getOrCreate()
# Load the data stored in LIBSVM format as a DataFrame.
data = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

# Automatically identify categorical features, and index them.
# We specify maxCategories so features with > 4 distinct values are treated as continuous.
featureIndexer =\
    VectorIndexer(inputCol="features", outputCol="indexedFeatures", maxCategories=4).fit(data)

# Split the data into training and test sets (30% held out for testing)
(trainingData, testData) = data.randomSplit([0.7, 0.3])

# Train a DecisionTree model.
dt = DecisionTreeRegressor(featuresCol="indexedFeatures")

# Chain indexer and tree in a Pipeline
pipeline = Pipeline(stages=[featureIndexer, dt])

# Train model.  This also runs the indexer.
model = pipeline.fit(trainingData)

# Make predictions.
predictions = model.transform(testData)

# Select example rows to display.
predictions.select("prediction", "label", "features").show(5)

# Select (prediction, true label) and compute test error
evaluator = RegressionEvaluator(
    labelCol="label", predictionCol="prediction", metricName="rmse")
rmse = evaluator.evaluate(predictions)
print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)

treeModel = model.stages[1]
# summary only
print(treeModel)
spark.stop()

output:


+----------+-----+--------------------+
|prediction|label|            features|
+----------+-----+--------------------+
|       0.0|  0.0|(692,[122,123,124...|
|       0.0|  0.0|(692,[123,124,125...|
|       0.0|  0.0|(692,[124,125,126...|
|       0.0|  0.0|(692,[124,125,126...|
|       0.0|  0.0|(692,[124,125,126...|
+----------+-----+--------------------+
only showing top 5 rows

Root Mean Squared Error (RMSE) on test data = 0.164399
DecisionTreeRegressionModel (uid=DecisionTreeRegressor_415194352f1feffc1231) of depth 1 with 3 nodes

Find full example code at “examples/src/main/python/ml/decision_tree_regression_example.py” in the Spark repo.

Random forest regression

随机森林是决策树的集成算法。随机森林包含多个决策树来降低过拟合的风险。随机森林同样具有易解释性、可处理类别特征、易扩展到多分类问题、不需特征缩放等性质。

随机森林分别训练一系列的决策树，所以训练过程是并行的。因算法中加入随机过程，所以每个决策树又有少量区别。通过合并每个树的预测结果来减少预测的方差，提高在测试集上的性能表现。

随机性体现：
1.每次迭代时，对原始数据进行二次抽样来获得不同的训练数据。

2.对于每个树节点，考虑不同的随机特征子集来进行分裂。

除此之外，决策时的训练过程和单独决策树训练过程相同。

对新实例进行预测时，随机森林需要整合其各个决策树的预测结果。回归和分类问题的整合的方式略有不同。分类问题采取投票制，每个决策树投票给一个类别，获得最多投票的类别为最终结果。回归问题每个树得到的预测结果为实数，最终的预测结果为各个树预测结果的平均值。

spark.ml支持二分类、多分类以及回归的随机森林算法，适用于连续特征以及类别特征。

Examples


from pyspark.ml import Pipeline
from pyspark.ml.regression import RandomForestRegressor
from pyspark.ml.feature import VectorIndexer
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("RandomForestRegressionExample").getOrCreate()
# Load and parse the data file, converting it to a DataFrame.
data = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

# Automatically identify categorical features, and index them.
# Set maxCategories so features with > 4 distinct values are treated as continuous.
featureIndexer =\
    VectorIndexer(inputCol="features", outputCol="indexedFeatures", maxCategories=4).fit(data)

# Split the data into training and test sets (30% held out for testing)
(trainingData, testData) = data.randomSplit([0.7, 0.3])

# Train a RandomForest model.
rf = RandomForestRegressor(featuresCol="indexedFeatures")

# Chain indexer and forest in a Pipeline
pipeline = Pipeline(stages=[featureIndexer, rf])

# Train model.  This also runs the indexer.
model = pipeline.fit(trainingData)

# Make predictions.
predictions = model.transform(testData)

# Select example rows to display.
predictions.select("prediction", "label", "features").show(5)

# Select (prediction, true label) and compute test error
evaluator = RegressionEvaluator(
    labelCol="label", predictionCol="prediction", metricName="rmse")
rmse = evaluator.evaluate(predictions)
print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)

rfModel = model.stages[1]
print(rfModel)  # summary only
spark.stop()

output:


+----------+-----+--------------------+
|prediction|label|            features|
+----------+-----+--------------------+
|       0.0|  0.0|(692,[95,96,97,12...|
|       0.0|  0.0|(692,[124,125,126...|
|       0.0|  0.0|(692,[126,127,128...|
|       0.0|  0.0|(692,[126,127,128...|
|       0.0|  0.0|(692,[126,127,128...|
+----------+-----+--------------------+
only showing top 5 rows

Root Mean Squared Error (RMSE) on test data = 0.193434
RandomForestRegressionModel (uid=RandomForestRegressor_4bfa98dd14412263de8e) with 20 trees

Find full example code at “examples/src/main/python/ml/random_forest_regressor_example.py” in the Spark repo.

Gradient-boosted tree regression

Gradient-boosted tree(GBTs)梯度提升树是一种决策树的集成算法。它通过反复迭代训练决策树来最小化损失函数。与决策树类似，梯度提升树具有可处理类别特征、易扩展到多分类问题、不需特征缩放等性质。Spark.ml通过使用现有decision tree工具来实现。

梯度提升树依次迭代训练一系列的决策树。在一次迭代中，算法使用现有的集成来对每个训练实例的类别进行预测，然后将预测结果与真实的标签值进行比较。通过重新标记，来赋予预测结果不好的实例更高的权重。所以，在下次迭代中，决策树会对先前的错误进行修正。

对实例标签进行重新标记的机制由损失函数来指定。每次迭代过程中，梯度迭代树在训练数据上进一步减少损失函数的值。spark.ml为分类问题提供一种损失函数（Log Loss），为回归问题提供两种损失函数（平方误差与绝对误差）。

Spark.ml支持二分类以及回归的随机森林算法，适用于连续特征以及类别特征。

注意：梯度提升树目前不支持多分类问题。

Examples

注意：对于这个示例数据集，GBTRegressor实际上只需要1次迭代，但通常情况并非如此。


from pyspark.ml import Pipeline
from pyspark.ml.regression import GBTRegressor
from pyspark.ml.feature import VectorIndexer
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("GBTRegressionExample").getOrCreate()
# Load and parse the data file, converting it to a DataFrame.
data = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

# Automatically identify categorical features, and index them.
# Set maxCategories so features with > 4 distinct values are treated as continuous.
featureIndexer =\
    VectorIndexer(inputCol="features", outputCol="indexedFeatures", maxCategories=4).fit(data)

# Split the data into training and test sets (30% held out for testing)
(trainingData, testData) = data.randomSplit([0.7, 0.3])

# Train a GBT model.
gbt = GBTRegressor(featuresCol="indexedFeatures", maxIter=10)

# Chain indexer and GBT in a Pipeline
pipeline = Pipeline(stages=[featureIndexer, gbt])

# Train model.  This also runs the indexer.
model = pipeline.fit(trainingData)

# Make predictions.
predictions = model.transform(testData)

# Select example rows to display.
predictions.select("prediction", "label", "features").show(5)

# Select (prediction, true label) and compute test error
evaluator = RegressionEvaluator(
    labelCol="label", predictionCol="prediction", metricName="rmse")
rmse = evaluator.evaluate(predictions)
print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)

gbtModel = model.stages[1]
print(gbtModel)  # summary only
spark.stop()

output:


+----------+-----+--------------------+
|prediction|label|            features|
+----------+-----+--------------------+
|       0.0|  0.0|(692,[100,101,102...|
|       0.0|  0.0|(692,[121,122,123...|
|       0.0|  0.0|(692,[122,123,124...|
|       0.0|  0.0|(692,[123,124,125...|
|       0.0|  0.0|(692,[124,125,126...|
+----------+-----+--------------------+
only showing top 5 rows

Root Mean Squared Error (RMSE) on test data = 0.288675
GBTRegressionModel (uid=GBTRegressor_4e5384caecb49745ae29) with 10 trees

Find full example code at “examples/src/main/python/ml/gradient_boosted_tree_regressor_example.py” in the Spark repo.

Survival regression

在spark.ml中，我们实施Acceleratedfailure time(加速失效时间模型)，对于截尾数据它是一个参数化生存回归的模型。它描述了一个有对数生存时间的模型，所以它也常被称为生存分析的对数线性模型。与比例危险模型不同，因AFT模型中每个实例对目标函数的贡献是独立的，其更容易并行化。

给定协变量的值x，对于可能的右截尾的随机生存时间，AFT模型下的似然函数如下：
AFT

可以证明AFT模型是一个凸优化问题，即是说找到凸函数ι(β,σ)的最小值取决于系数向量β以及尺度参数σ的对数.其中实现的优化算法为L-BFGS，该实现与R的生存函数survreg的结果相匹配。

当使用无拦截的连续非零列训练AFTSurvivalRegressionModel时，Spark MLlib为连续非零列输出零系数。这种处理与R中的生存函数survreg不同。

Examples


from pyspark.ml.regression import AFTSurvivalRegression
from pyspark.ml.linalg import Vectors
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("SurvivalRegressionExample").getOrCreate()
training = spark.createDataFrame([
    (1.218, 1.0, Vectors.dense(1.560, -0.605)),
    (2.949, 0.0, Vectors.dense(0.346, 2.158)),
    (3.627, 0.0, Vectors.dense(1.380, 0.231)),
    (0.273, 1.0, Vectors.dense(0.520, 1.151)),
    (4.199, 0.0, Vectors.dense(0.795, -0.226))], ["label", "censor", "features"])
quantileProbabilities = [0.3, 0.6]
aft = AFTSurvivalRegression(quantileProbabilities=quantileProbabilities,
                            quantilesCol="quantiles")

model = aft.fit(training)

# Print the coefficients, intercept and scale parameter for AFT survival regression
print("Coefficients: " + str(model.coefficients))
print("Intercept: " + str(model.intercept))
print("Scale: " + str(model.scale))
model.transform(training).show(truncate=False)
spark.stop()

output:


Coefficients: [-0.496304411053,0.198452172529]
Intercept: 2.638089896305637
Scale: 1.5472363533632303
+-----+------+--------------+------------------+---------------------------------------+
|label|censor|features      |prediction        |quantiles                              |
+-----+------+--------------+------------------+---------------------------------------+
|1.218|1.0   |[1.56,-0.605] |5.718985621018948 |[1.160322990805951,4.99546058340675]   |
|2.949|0.0   |[0.346,2.158] |18.07678210850554 |[3.6675919944963185,15.789837303662035]|
|3.627|0.0   |[1.38,0.231]  |7.381908879359957 |[1.4977129086101564,6.448002719505488] |
|0.273|1.0   |[0.52,1.151]  |13.577717814884515|[2.754778414791514,11.859962351993207] |
|4.199|0.0   |[0.795,-0.226]|9.013087597344821 |[1.82866218773319,7.8728164067854935]  |
+-----+------+--------------+------------------+---------------------------------------+

Find full example code at “examples/src/main/python/ml/aft_survival_regression.py” in the Spark repo.

Isotonic regression

保序回归是回归算法的一种。保序回归给定一个有限的实数集合(Y=y1,y2,…,yn)代表观察到的响应,以及(X=x1,x2,…,xn)代表未知的响应值，训练一个模型来最小化下列方程：
f(x) = ∑ωi(yi-xi)²,其中wi为权重是正值，其结果方程称为保序回归，而且其解是唯一的。它可以被视为有顺序约束下的最小二乘法问题。实际上保序回归在拟合原始数据点时是一个单调函数。我们实现池旁者算法，它使用并行保序回归。训练数据是DataFrame格式，包含标签、特征值以及权重三列。另外保序算法还有一个参数名为isotonic，其默认值为真，它指定保序回归为保序（单调递增）或者反序（单调递减）。

训练返回一个保序回归模型，可以被用于来预测已知或者未知特征值的标签。保序回归的结果是分段线性函数，预测规则如下：

如果预测输入与训练中的特征值完全匹配，则返回相应标签。如果一个特征值对应多个预测标签值，则返回其中一个，具体是哪一个未指定。
如果预测输入比训练中的特征值都高（或者都低），则相应返回最高特征值或者最低特征值对应标签。如果一个特征值对应多个预测标签值，则相应返回最高值或者最低值。
如果预测输入落入两个特征值之间，则预测将会是一个分段线性函数，其值由两个最近的特征值的预测值计算得到。如果一个特征值对应多个预测标签值，则使用上述两种情况中的处理方式解决。

Examples

有关API的更多详细信息，请参阅IsotonicRegressionPython文档。


from pyspark.ml.regression import IsotonicRegression
from pyspark.sql import SparkSession

spark = SparkSession.builder.appName("IsotonicRegressionExample").getOrCreate()
# Loads data.
dataset = spark.read.format("libsvm")\
    .load("data/mllib/sample_isotonic_regression_libsvm_data.txt")

# Trains an isotonic regression model.
model = IsotonicRegression().fit(dataset)
print("Boundaries in increasing order: %s\n" % str(model.boundaries))
print("Predictions associated with the boundaries: %s\n" % str(model.predictions))

# Makes predictions.
model.transform(dataset).show()
spark.stop()

output:


Boundaries in increasing order: [0.01,0.17,0.18,0.27,0.28,0.29,0.3,0.31,0.34,0.35,0.36,0.41,0.42,0.71,0.72,0.74,0.75,0.76,0.77,0.78,0.79,0.8,0.81,0.82,0.83,0.84,0.85,0.86,0.87,0.88,0.89,1.0]

Predictions associated with the boundaries: [0.157152712941,0.157152712941,0.189138196,0.189138196,0.20040796,0.29576747,0.43396226,0.5081591025,0.5081591025,0.54156043,0.550484446667,0.550484446667,0.563929967,0.563929967,0.566037736667,0.566037736667,0.56603774,0.57929628,0.64762876,0.66241713,0.67210607,0.67210607,0.674655785,0.674655785,0.73890872,0.73992861,0.84242733,0.89673636,0.89673636,0.90719021,0.9272055075,0.9272055075]

+----------+--------------+-------------------+
|     label|      features|         prediction|
+----------+--------------+-------------------+
|0.24579296|(1,[0],[0.01])|0.15715271294117644|
|0.28505864|(1,[0],[0.02])|0.15715271294117644|
|0.31208567|(1,[0],[0.03])|0.15715271294117644|
|0.35900051|(1,[0],[0.04])|0.15715271294117644|
|0.35747068|(1,[0],[0.05])|0.15715271294117644|
|0.16675166|(1,[0],[0.06])|0.15715271294117644|
|0.17491076|(1,[0],[0.07])|0.15715271294117644|
| 0.0418154|(1,[0],[0.08])|0.15715271294117644|
|0.04793473|(1,[0],[0.09])|0.15715271294117644|
|0.03926568| (1,[0],[0.1])|0.15715271294117644|
|0.12952575|(1,[0],[0.11])|0.15715271294117644|
|       0.0|(1,[0],[0.12])|0.15715271294117644|
|0.01376849|(1,[0],[0.13])|0.15715271294117644|
|0.13105558|(1,[0],[0.14])|0.15715271294117644|
|0.08873024|(1,[0],[0.15])|0.15715271294117644|
|0.12595614|(1,[0],[0.16])|0.15715271294117644|
|0.15247323|(1,[0],[0.17])|0.15715271294117644|
|0.25956145|(1,[0],[0.18])|        0.189138196|
|0.20040796|(1,[0],[0.19])|        0.189138196|
|0.19581846| (1,[0],[0.2])|        0.189138196|
+----------+--------------+-------------------+
only showing top 20 rows

Find full example code at “examples/src/main/python/ml/isotonic_regression_example.py” in the Spark repo.

更多请查阅spark.ml-classification-regression

Classfication

Logistic Regression

Binomial Logistic Regression

Multinomial Logistic Regression

Decision Tree Classifier

Random Forest Classifier

Gradient-Boosted Tree Classifier

Multilayer Perception Classifier

Linear Support Vector Machine

One-vs-Rest Classifier(又叫 One-vs-All)

Naive Bayes

Regression

Linear regression

Generalized linear regression

Decision tree regression

Random forest regression

Gradient-boosted tree regression

Survival regression

Isotonic regression

结束